La ampliación de avenidas y el fútbol

¿Cuál es la primera movida que tiene el entrenador de un equipo de fútbol, cuando se enfrenta a otro donde hay un crack, un jugador excepcional, un Messi, digamos? ¿Y qué es lo que solemos hacer nosotros, como conductores, con las avenidas particularmente grandes, que ―en principio― tienen la prioridad sobre las demás? Aunque las dos preguntas parezcan estar desconectadas por completo, el trasfondo es el mismo: la paradoja de Braess. Sí, yo sé, vengo hablando de esto desde hace varios posts, pero es que la importancia de este concepto trasciende una sola idea. Más aún cuando uno ve que las gestiones municipales se empeñan en perseguir este modelo obsoleto y anacrónico de destruirconstruir nuestra ciudad atravesándola aleatoriamente con autopistas y bypasses. Pero bueno, mi intención aquí es explorar la analogía con el fútbol, que ya el tema del transporte ha sido bastante tocado aquí, aquí y aquí. Y también aquí. Y por aquí.

Brian Skinner, de la Universidad de Minnesota, publicó este artículo hace unos años en el Journal of Quantitative Analysis in Sports. «The price of anarchy in basketball» apela a entender ese juego y la dinámica de los pases entre jugadores, a partir de compararlos con una red vehicular y aplicar ahí algunos conceptos de teoría de juegos. Como nosotros no somos muy dados a ese deporte, me tomaré la libertad de adaptar la explicación a algo que nos es más familiar: el fútbol. Había empezado la idea a partir de la marcación desmedida que suelen hacer unos equipos a ciertos jugadores adversarios. Esta decisión suele ser adecuada cuando sus equipos centralizan la mayoría de sus movimientos a través de su jugador estrella, pues terminan ahogándose solos al no poder generar una situación de gol nunca.

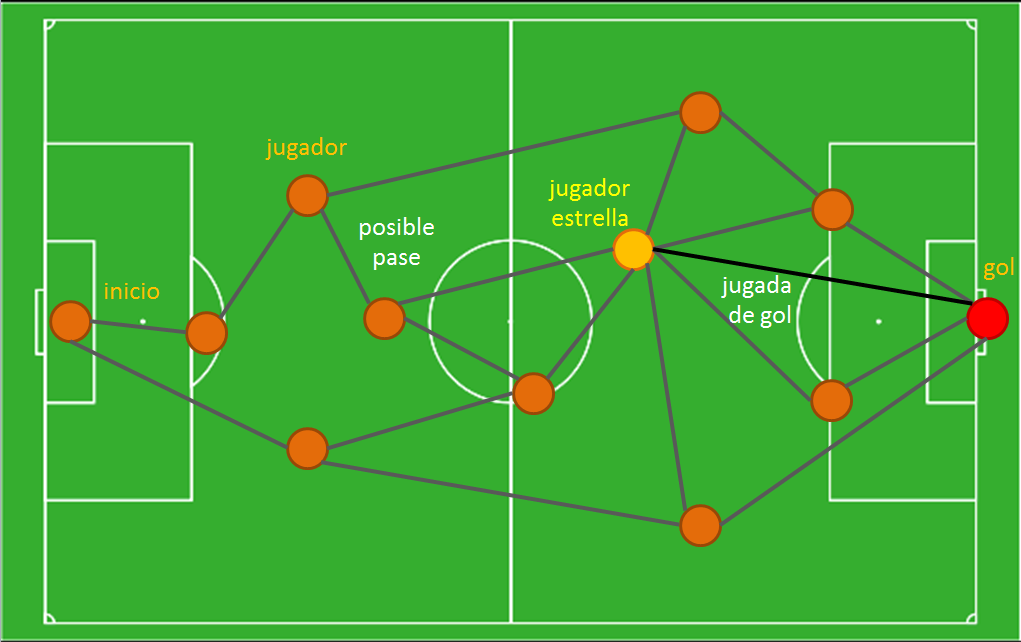
¿Cómo es que esto puede entenderse desde las redes vehiculares? La figura es relativamente sencilla: pensemos que el arco de un equipo es su punto de inicio, el arco rival el punto final, y cada posible pase entre dos jugadores cualesquiera es una avenida. El entramado vial sería entonces una proyección de todas las posibles jugadas que permiten llegar de un arco a otro a través de los pases entre jugadores de un equipo. Algo así como lo que se ve a continuación:

En el diagrama se muestran posibles pases entre todos los jugadores del equipo, por medio de líneas grises, que eventualmente terminan en un gol (el círculo rojo). El modelo es una simplificación del juego, evidentemente, pero permite captar la idea. Y la realidad parte del mismo principio, solo que es algo más entrevesada. Digamos que el jugador estrella es el que está marcado de amarillo y tiene una probabilidad mayor que sus compañeros de realizar un gol directamente, cosa que indicamos por medio de la línea negra. La facilidad de cada jugador de realizar un pase puede incluir no solo su habilidad, sino la marcación promedio de un oponente, de modo que podemos asimilar al otro equipo dentro de este modelo. Para ello consideramos que la frecuencia con que un jugador recibe pases irá decreciendo en el tiempo su probabilidad de realizarlos efectivamente. Ahora se entiende el problema, ¿verdad? Los mejores jugadores tenderán a recibir más pases, dado que en teoría son más efectivos, pero esta preferencia incita una marcación desmedida, lo que los empieza a hacer ineficientes. En el caso de un Messi, cuya posesión del balón se asume casi como un gol hecho, el resultado es que su equipo termina ahogándose rápidamente si no se distribuye en más direcciones.

¿Cómo se relaciona esto con las avenidas? Nuevamente adaptaré un ejemplo de Skinner a nuestra realidad: tomemos la av. Javier Prado, a la altura del cruce con la av. Camino Real. Digamos que estamos ahí y queremos llegar al bloque de tiendas de San Isidro, o acceder al cruce de la vía Expresa con la av. Canaval y Moreyra. Estos puntos se indican en la imagen siguiente por medio de A y B. Existe una ruta obvia, amplia, pero larga ―indicada con azul en la figura― que implica seguir por la av. Javier Prado hasta llegar a la av. Rivera Navarrete, para luego bajar por ella y llegar directamente hasta B. Digamos que esa ruta toma siempre 20 min. independientemente de cuántos vehículos transiten por ahí. Por otro lado, existe una segunda ruta ―indicada en negro― que implica meterse entre calles pequeñas y desembocar finalmente a través de la Ca. Chinchón. Esta segunda ruta puede recorrese en 10 min. ―digamos― si no la usa nadie más, pero el tiempo empieza a crecer a medida que aumentan los carros que circulan por ella. Digamos que en el límite, con 20 vehículos, el tiempo crece en 10 min. Eso nos lleva a la siguiente situación: si tenemos 20 vehículos circulando de A hacia B, ¿qué ruta deberían tomar?

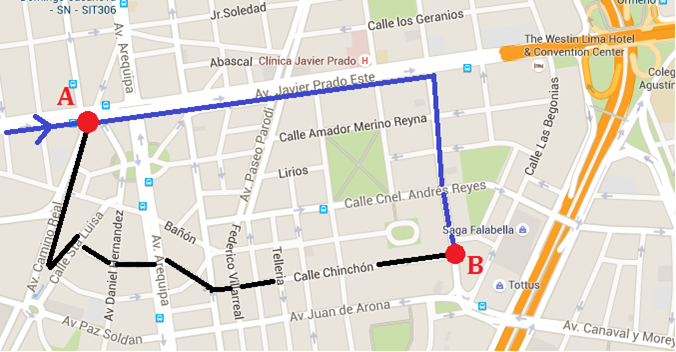
El problema se resuelve muy fácilmente si se apela a que los conductores son individuos que buscan optimizar su meta personal: llegar lo más pronto posible de A a B. Para ninguno, nunca existirá estímulo para tomar la ruta de la Javier Prado, porque siempre demorará más, o en el peor de los casos igual, que la ruta por Chinchón. El problema es que esa elección lleva a un tiempo global medio de 20 min. para todos los vehículos. Pero si alguno decidiera irse por la Javier Prado, ¡la media global bajaría! De hecho, puede demostrarse que la distribución que minimiza el tiempo promedio global es 10 vehículos yendo por la av. Javier Prado y 10 yendo por la Ca. Chinchón. Esa distribución hace que el tiempo medio global sea de 12.5 min. ¡Un 37.5% menos que los 20 min. que se obtienen con la elección egoísta! Y lo paradójico está en que cualquier vehículo que decida cambiar de la ruta azul a la negra, aunque mejore su tiempo, lo hará a costa de perjudicar el de todos los demás.

La cantidad de lecciones que podemos obtener de aquí es fantásticamente amplia. No solo rompe con esa idea absurda de que la única manera de optimizar el beneficio global es a través de optimizar aisladamente los beneficios individuales, sino que demuestra que el límite al que converge un sistema auto-organizado no necesariamente es el óptimo. La regulación, pues, es a veces necesaria, amigos liberales. Para el bien de todos.

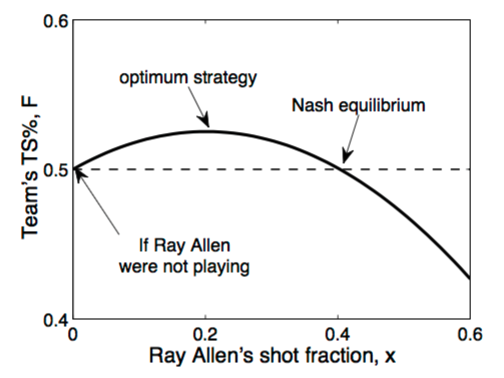
¿Y cómo regresamos de aquí al ejemplo del fútbol? Pues con algo que todos los que practican y disfrutan de ese deporte debe(ría)n saber: no le puedas dar todos los pases a tu mejor jugador; no puedes esperar que Messi te salve el partido. O, en todo caso, todos los partidos. Concentrar la atención de todas las jugadas en un solo jugador terminará por saturarlo con los defensas del equipo contrario y su rendimiento decrecerá hasta volverlo inútil. En su paper, Skinner desarrolla un ejemplo a partir de un jugador y equipo específicos, cuyo flavor es el siguiente:

Es discutible que la forma de la curva sea más o menos pronunciada; eso dependerá de los valores específicos que tenga un modelo particular. Lo que deja como conclusión el ejemplo de Skinner y, finalmente, la paradoja de Braess, es que la optimización global de un sistema conformado por elementos individuales y personalistas no necesariamente va a alcanzarse desde una optimización local. Ni siquiera cuando exista un elemento o combinación de elementos que sean mejores que el resto.

Y esa conclusión no es para nada obvia.